Post-Keynesians unnecessarily worry a lot about the paradox of profits. This post is on my thoughts on the paradox. In my view, there is no paradox at all. It is simply the case of not looking at all the parts of the system of national accounts/flow of funds.

Although Post-Keynesians use Kalecki’s profit equation in which the government deficit adds to profits, the statement of the paradox is for a pure credit economy. But in any case, there is none.

Let us assume that at the beginning of the ‘circuit’, production firms need an initial loan to pay the wage bill WB in advance. Households receive the wages and consume C and allocate their saving in financial assets (households don’t buy houses). The two financial assets are money and equities so:

WB − C = ΔM + ΔE

Production firms’ profits F_f  is:

F_f  = C + I – WB − r_lL

Here, I is the gross fixed capital formation of production firms or investment, L is the outstanding loan of firms from the banking system and r_l is the rate of interest on these loans.

Now assume all investment is financed by issuing equities (i.e., ΔE = I). With a small amount of algebra:

F_f  = − ΔM  − r_lL

So this is the “paradox”.

Now there are several things wrong with this. The simplest is that profits are actually paid to households and there’s a term for change in inventories missing in the right hand side. If profits are not paid, they are retained and investment is then financed by both issuing equities and retained earnings. So ΔE ≠ I. 

There is an alternative way of stating the “paradox” which says: if firms inject money at the start of the production process, how do they recover more money at the end of the process? This seems to confuse what is known as operating surplus in the system of national accounts (such as in the 2008 SNA or earlier versions) with the surplus on the financial account.

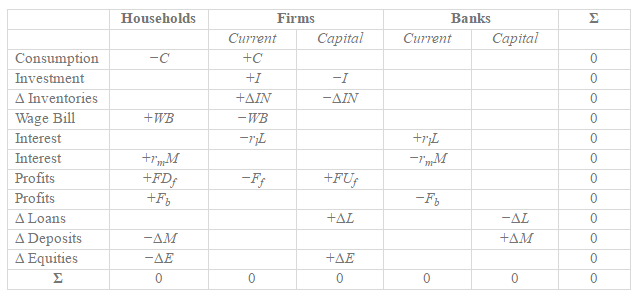
So let us redo this. Here is the transactions flow matrix for the economy (assuming away banks’ undistributed profits):

First assume all profits are distributed (i.e., FU_f = 0 and FD_f = F_f).

So:

 WB + r_mM + F_f  + F_b − C = ΔM + ΔE

F_f  = C + I + ΔIN − WB − r_lL

Then assuming ΔE = I and a bit of algebra,

ΔIN = ΔM

In other words, there is no paradox at all. F_f  has simply dropped out. All this means is that if households wish to hold more of their assets in deposits instead of equities, firms will be left with more inventories.

Of course, you might ask, “how have you assumed that profits are distributed when there is a paradox?”. The answer is that I haven’t done anything self-inconsistent. More consistency checks would be via constructing a dynamic model and check if it solves but assuming it does, the above static analysis is good enough. There is no paradox to begin with.

So in the above, although there was no paradox of profits, there was still a pressure on output and hence profits—if households wished to hold more of their wealth in deposits and reduce their preference to buy equities, firms will be left with more inventories and will have to reduce investment. This reduction in investment happens because of two reasons – a fall in equity prices and a fall in output leading to a fall in firms’ expectations of sales. Of course, this can be seen via writing dynamic models, and one shouldn’t rely on identities. But bank loans will be useful here and so higher preference for ‘money’ needn’t necessarily lead to a fall in output. If households wish to hold more money instead of other assets, firms may switch to bank loans and this process creates deposits.

But let’s for the moment still assume that investment is not financed via bank loans but via issuance of equities and retained earning. In this case,

WB + r_mM + FD_f  + F_b − C = ΔM + ΔE

F_f  = C + I + ΔIN − WB − r_lL

but also,

ΔE = I − FU_f 

and with some algebra,

ΔIN = ΔM

Again, no paradox. At all!

Now in the final case, assume that production firms use bank loans to finance investment in addition to financing it via equities. The equations are:

WB + r_mM + FD_f  + F_b − C = ΔM + ΔE

F_f  = C + I + ΔIN − WB − r_lL

ΔE = I − ζΔL − FU_f 

where 0 < ζ < 1 is that part of ΔL used for investment expenditure. In this case,

ΔIN + ζΔL = ΔM

So if households wish to hold more deposits, firms will switch to bank loans without any drop in inventories, output or expectations, with the qualification of course that bank credit is available.

Some have suggested (via Kalecki’s profit equation) that the paradox can be resolved only because of government deficits. This is not needed at all because there is no paradox. So around the turn of the millennium, the US government had its budget balance in surplus and the nation’s current account balance of international payments was in deficit over many quarters. Yet US firms made profits and were able to distribute them.

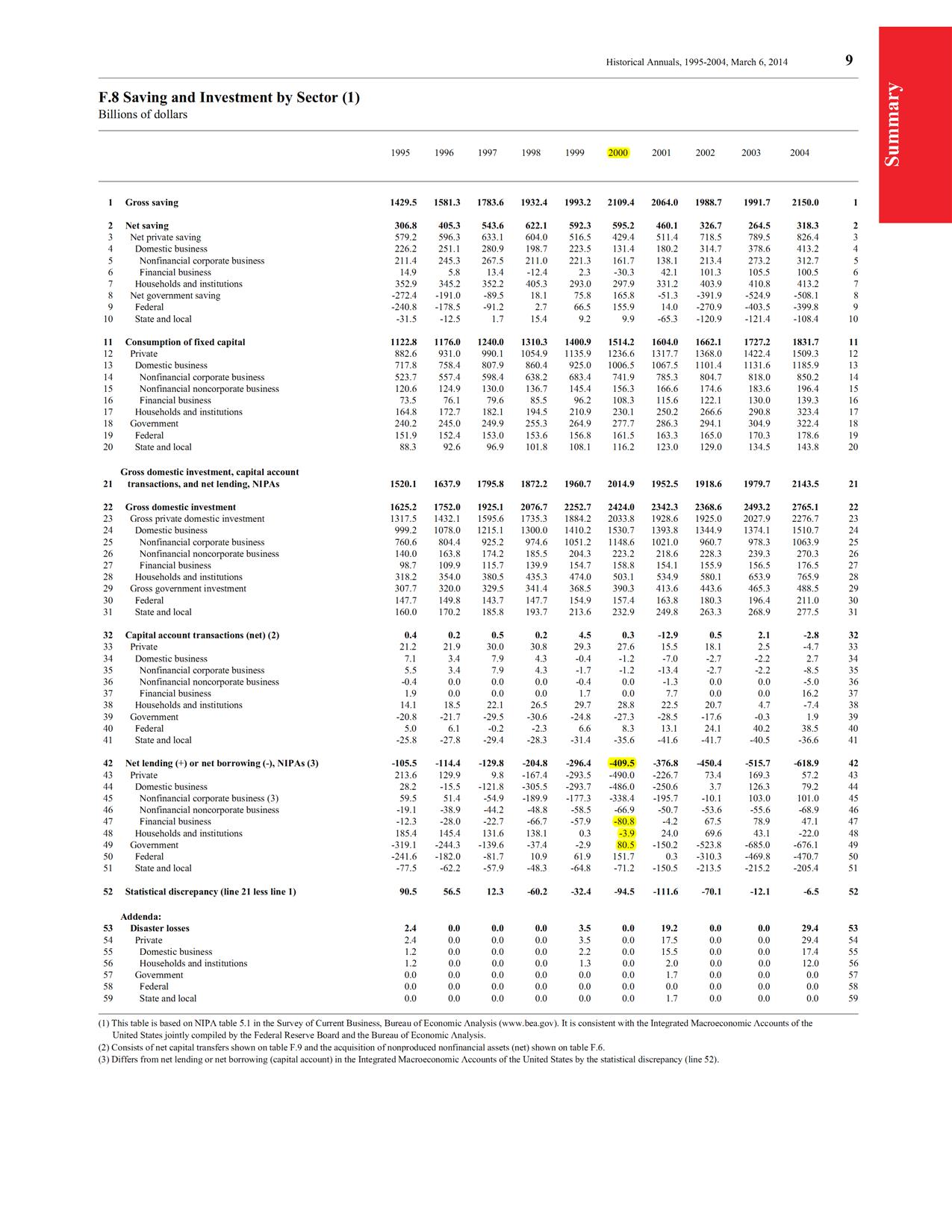
See the data below: the first one highlights in yellow the current account balance (line 42) and the budget balance (line 49) and also the fact that the financial balances of other sectors (lines 47/48) were low negative compared to profits numbers in question (source Z.1):

 (click to expand and click again)

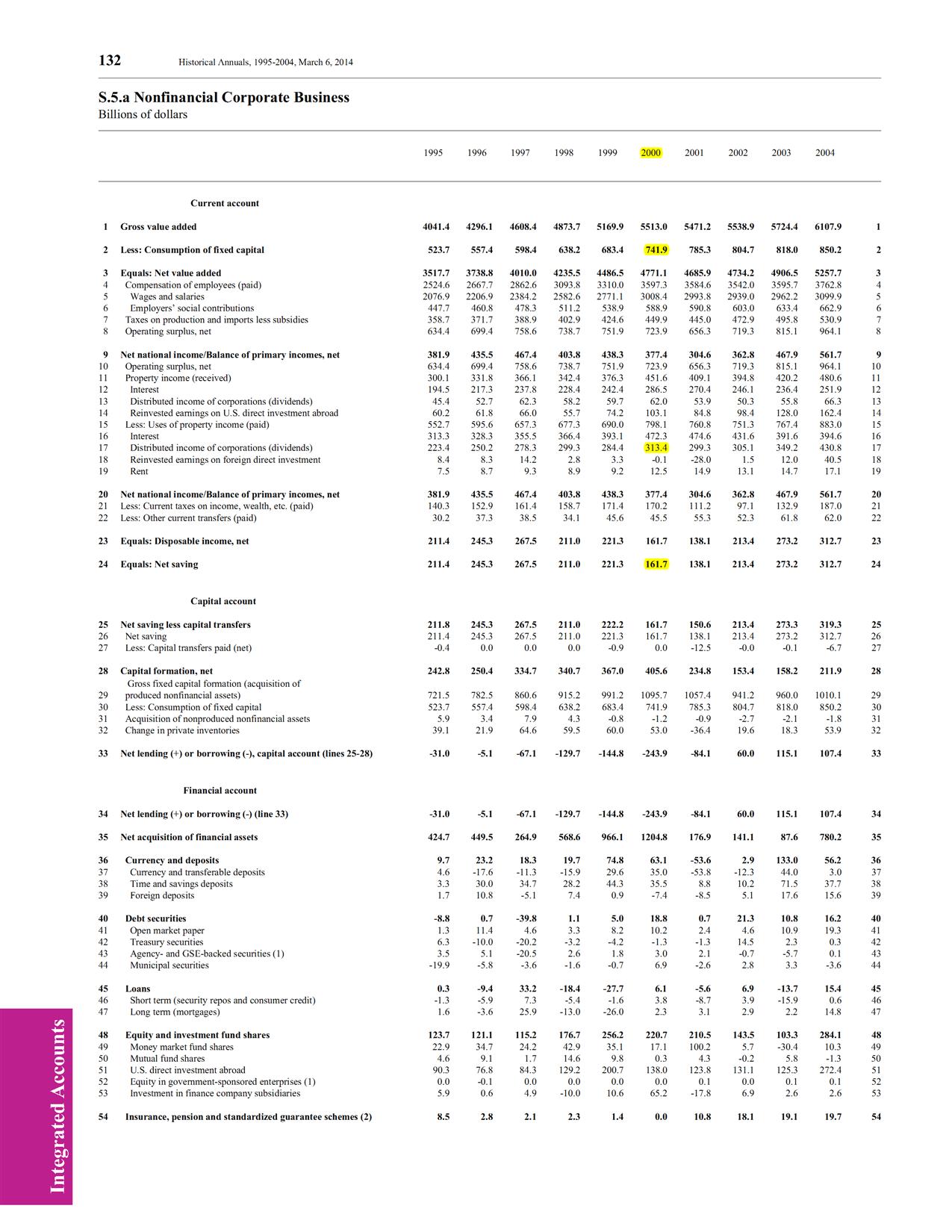
the second one shows the net undistributed profits (undistributed profits less depreciation) (line 24), distributed profits (line 17) and depreciation (line 2) from which profits can be calculated, implying budget deficit and/or positive current account balance of payments is not needed to resolve the paradox of profits (because there is none to begin with).

 (click to expand and click again)

Of course, fiscal policy was tight around the time (although the budget balance is a poor measure of this) and this led to a fall in output soon, but that issue shouldn’t be confused with the paradox of profits.

Conclusion

One does not simply confuse operating surplus and surplus on the financial account of the system of national accounts. There is no resolution of the paradox of profits because there is none to begin with.